Notes on Hierarchal Reasoning Model
aka what can we learn from the brain!
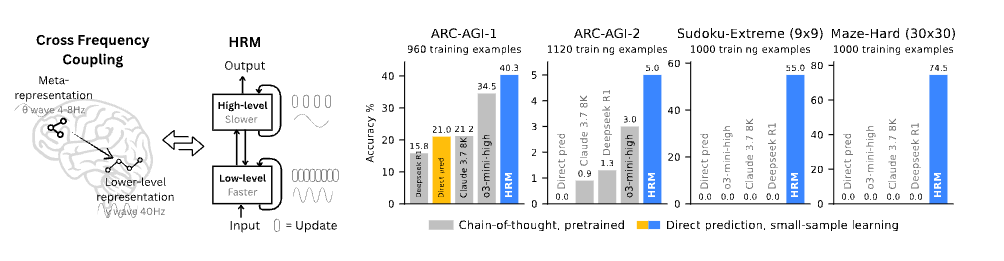
I recently read this paper that’s been in the news. Apparently, with 27 million parameters, they beat SOTA models on tasks that require recurrent computation (like solving sudoku puzzles or maze solving).
It’s a fascinating paper with rich, detailed references to brain and an extensive references list. Plus, the code is open source.
Following is my notes on the paper. I recommend first skimming through the paper and only then going through the notes.
There are four components in the architecture
Input network -> transforms input to input representation
Low-level recurrence -> takes input representation, hidden state of high-level recurrence last step (fixed for all steps), hidden state of low level recurrence previous step -> outputs next hidden state of low level recurrence
Runs for T steps
High-level recurrence -> takes hidden state of high-level recurrence last step, hidden state of low level recurrence last step of previous step -> outputs next hidden state of high level recurrence
Runs for N steps, once after each T steps of low-level recurrence
Output network -> takes last state of high level recurrence -> outputs output
One forward pass is N*T steps
T low level recurrence steps
N high level recurrence steps, once each T steps
Gradient updates
Not back-propagated in time
Just apply gradients to last step of recurrence steps
Due to fixed point theorem where you can simply compute d(hidden state)/d(parameters) without stepping through intermediate steps
Successive diffusion like multiple forward passes
Before first step, initialize starting hidden states as random values
Take hidden state from previous forward pass (final step) into the next step first value
Learn a separate head on when to stop
They use Q-learning heads to predict values of stopping or continuing
Loss is done on all steps, and they combine prediction loss with Q-learning loss
Questions in my head
Why just backpropagating to last step of hidden works
Implicit value theorem: still not clear about the theory
How is input transformed and actual implementation of input and output states
Input is of a sequence of x1, x2, … xn, each of these is transformed into a hidden state so we get [n, d] vector
E.g. for sudoku (9x9), you get 81 sequences and each digit can be represented using one of the 10 tokens [0 to 9 + one blank]
What does L and H network look like
We simply add up representations
Hidden states are added to the input states
Output is hidden states
And then we step through time
These networks use full cross-attention (not masked one)
As these are not auto-regressive (but can be made into those)
Extending / testing the model
Since the code is open source, if anyone’s interested, it’d be cool to evaluate the model on following tasks:
Multiplying two numbers → LLMs fail to generalize to arbitrary number of digits, will this model do any better?
My guess is not as fundamentally this model is similar to a transformer with hidden state fed back into the network for multiple steps and then decoding answer using final hidden state
Language modeling → they didn’t do language modeling, but I think someone can attempt doing character level modeling on a dataset like TinyStories dataset
This will likely require causal masking in the low and high level recurrence networks
The author, Paras Chopra, is founder and researcher at Lossfunk.

Best read, clear explanation