Notes on Tiny Recursion Network

aka how a 7M parameter network gets SOTA on Sudoku-Extreme with 87% accuracy

Earlier, we published our notes on Hierarchal Reasoning Model. It was a fascinating take on how recursion with a small network can help achieve strong performance on ARC-AGI, Sudoku and Maze Following tasks.

Recently, an improved version of it was proposed called Tiny Recursion Network. The paper itself is easy to read, so I encourage you to first read it.

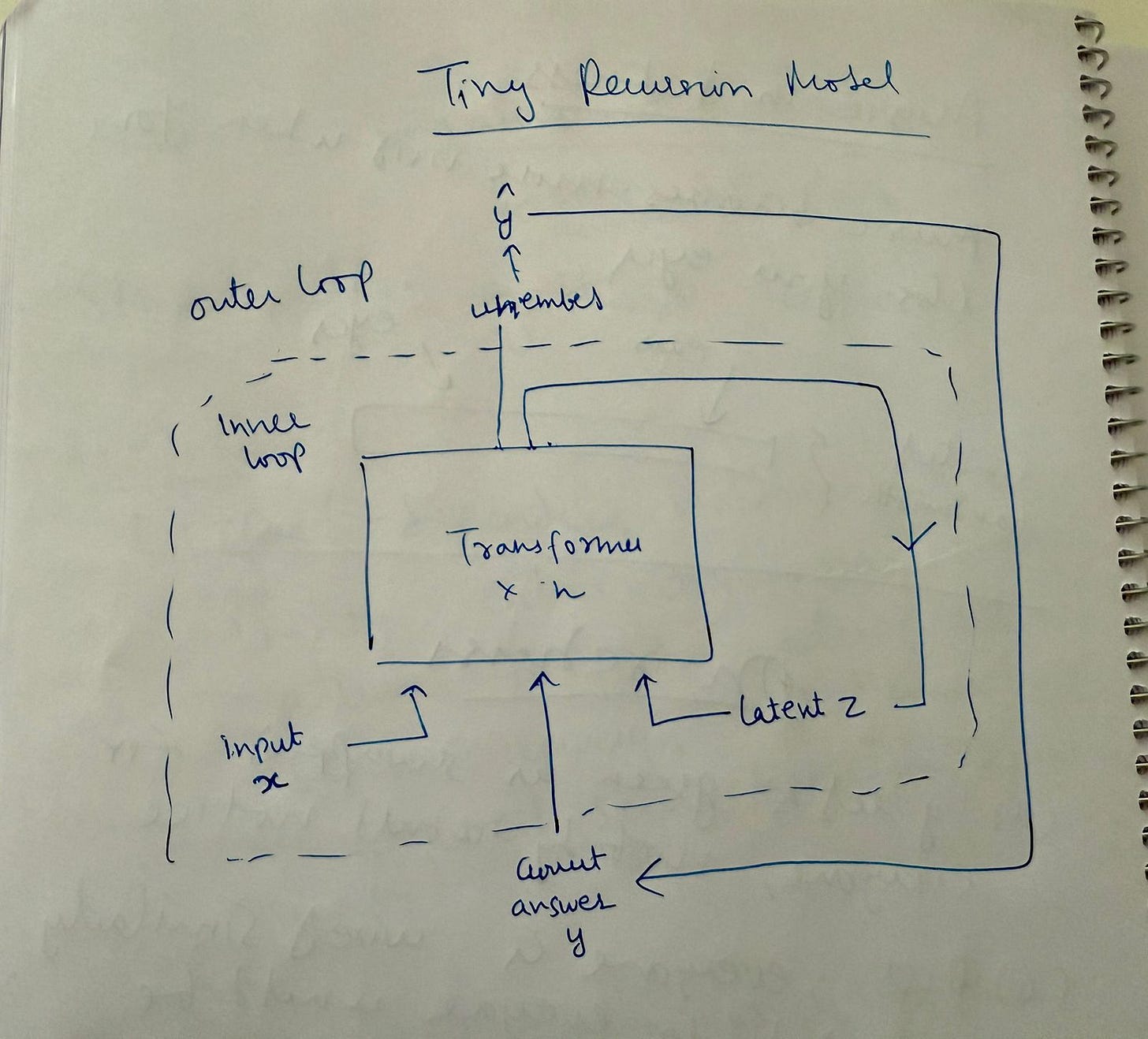
What it does is simple and can be illustrated by the following image:

How it works

There are two loops in the network and the pseudocode goes like this.

• Fix a network (say transformer blocks x 2)

• Embed / prepare input, initialize latent z and initialize answer attempt y

• Inner loop

  • Run T-1 times without gradients:

    • y,z = network(x,y,z) #this refines the answer

  • Run 1 time:

    • y,z = network(x,y,z)

    • y_hat = unembed(y)

    • q_hat = q_head(y) #this is used to decide to early stop

    • Calculate softmax cross entropy loss of y_hat with y_true (from training) and add to loss

    • Calculate binary cross entropy loss of q_hat against whether y_hat is exactly equal to y_true

    • Back prop loss

    • One step gradient

    • Optimizer reset gradients

  • if q_hat > 0: #since q_hat is a logit, q_hat>0 corresponds to sigmoid(q_hat) > 0.5, i.e. closer to accurate prediction

    • break

• Outer loop: #once per training example

  • Run inner loop for N_supervision (16) steps or until break happens

Intuition for why it works:

• Inner loop is training the network to explore: how to move wrong answer towards the correct answer, given an output

  • Imagine there was only a single step in the inner loop and we backprop through it, what it does then is to take initial (wrong) answer towards correct one (from data)

    • Since single step is optimized to push wrong answer y to y_true, applying it multiple times should help it continue to explore (we save on backprop since single step is optimized to do the same)

• Outer loop is to help refine somewhat correct answer to more correct answer

  • Since we backprop each time outer loop happens and with each outer loop previous answer is input to the network, we’re teaching the network to refine somewhat correct answer to even more correct answer

• The effect of both loops is that network learns to both explore and refine

Why less is more

In the paper they show more layers overfit and generalize worse. So, my intuition is that recursion is powerful because you learn the function once but then use it multiple times, this trades off parameters (that can memorize stuff) into computation (fewer parameters).

With more parameters, layer N, parameter X can memorize (especially if data is sparse), but with fewer parameters and recursion, you’re forcing the network to learn what needs to happen to iterate to a better solution.

Note that this approach will work for problems requiring iteration (application of the same thing over and over again) like multiplication or addition, but won’t work for problems that require other ways of solving (like classification or generation). So while a useful idea it’s not a universal panacea.

---

The author, Paras Chopra, is founder and researcher at Lossfunk.